
MỘT SỐ VÍ DỤ VỀ HỆ PHƯƠNG TRÌNH BẬC HAI HAI ẨN
I/Mục tiêu:
Giúp học sinh :
Về kiến thức : Nắm được các phương pháp chủ yếu giải hệ phương trình bậc hai hai ẩn , nhất là hệ phương trình đối xứng.
Về kĩ năng : Biết cách giải một số dạng hệ phương trình bậc hai hai ẩn , đặc biệt là các hệ gồm một phương trình bậc nhất và
một phương trình bậc hai , hệ phương trình đối xứng .
Về thái độ : Cẩn thận ,chính xác .
II/Chuẩn bị của giáo viên và học sinh :
+HS : Đọc trước bài mới .
+GV : Giáo án , phiếu học tập .
III/ Phương pháp :
Đặt vấn đề - hoạt động nhóm .
IV/ Những điểm cần lưu ý :
Nhận xét : nếu một hệ phương trình đối xứng với hai ẩn có nghiệm là (a,b) thì cũng có nghiệm là (b,a) , điều này rất có ích
cho HS vì : HS có thể căn cứ vào đó để tự kiểm tra mình giải hệ phương trình có gì sai sót không , nếu tìm thấy
nghiệm (a,b) mà không thấy nghiệm (b,a) thì có thể khẳng định lời giải có vấn đề . Tuy nhiên nếu có đầy đủ các
nghiệm (a,b) và (b,a) thì vẫn chưa thể khẳng định lời giải là chắc chắn đúng .
V/ Tiến hành bài giảng :
Chia lớp thành 3 nhóm , thực hiên 3 phiếu học tập sau :
Phiếu 1:
1/Nêu các phương pháp thường dùng để giải một hệ phương trình đã học ở lớp 9.
2/ Giải hệ phương trình sau :

Phiếu 2:
Giải hệ phương trình sau ;

Phiếu 3:
Giải hệ phương trình sau :

Sau khi phân công nhiệm vụ cho mỗi nhóm xong , GV hướng dẫn cho HS thực hiện các hoạt động :
| HOẠT ĐỘNG GIÁO VIÊN | HOẠT ĐỘNG HỌC SINH | GHI BẢNG |
| H1: Gọi đại diện nhóm 1 trình bày hoạt động của nhóm : -Nêu các phương pháp thường dùng để giải hệ phương trình quen thuộc. -Nhận xét về các phương trình có trong hệ đã cho ? -Đối với hệ dạng này thì giải như thế nào? | -phương pháp thế. -phương pháp cộng đại số . -phương pháp đặt ẩn phụ . -Hệ gồm một phương trình bậc nhất và một phương trình bậc hai. -Từ phương trình bậc nhất , tính y theo x (hoặc x theo y ) rồi thay vào phương trình bậc hai:Hệ đã cho tương đương với: 
| MỘT SỐ VÍ DỤ VỀ HỆ PHƯƠNG TRÌNH BẬC HAI HAI ẨN . Ví dụ 1: Giải hệ phương trình sau: ![clip_image002[1] clip_image002[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjWmZ32af29UAyMAmiLLXL1wxq9f9wdWQyK6uSXh-RLAbklHe3KK7SLLy_WY7kg_MgjHIpcOzb8tGCLXE06oz0ibjGyj-tAJsUG2I3MirIsL6I3oZLw_RFOgawQCmO1q3ZRE3G77eOJ4yAo/?imgmax=800) (I) (I)
Nghiệm của hệ là (1,-1) ;  |
| H2: Gọi đại diện nhóm 2 trình bày : -Có nhận xét gì về vai trò của x,y . -Thử thay x bởi y và thay y bởi x , em có nhận xét gì ? -Hệ (II) được gọi là hệ phương trình đối xứng. -Nếu (x0,y0) là nghiệm của hệ thì (y0,x0) cũng là nghiệm . -Giải bằng cách đặt ẩn phụ S = x +y , P = xy. -Biến đổi hệ (II) thành hệ theo S,P mà đã biết cách giải . Nhận xét : Với S = 3 , P = 2 thì tìm được x , y . Với S = -6 , P = 11 thì không có x , y . | -Trong hệ (II) vai trò của x , y là như nhau . -Mỗi một phương trình trong hệ sẽ không thay đổi .  Đặt S = x+y ; P = xy , thay vào (II.1) ta được hệ :  Giải hệ này ta được :  hoặc hoặc  +Với S = 3 , P = 2 thì x , y là nghiệm của phương trình : X2 – 3X + 2 = 0 , giải phương trình này ta được X = 1 , X = 2 , suy ra : 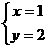 hoặc hoặc  là nghiệm của hệ (II) là nghiệm của hệ (II)
+Với S = -6 , P = 11 thì x, y là nghiệm của phương trình X2 +6X +11=0 , phương trình này vô nghiệm . Kết luận : Nghiệm của hệ (II) là : ![clip_image020[1] clip_image020[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhTVfyNVbncthe9T1W1J6HchPkFVYGMMBU6oP9UNccsgnPIF8Wo-RX8y3CMgHgKPckvP_Q3TvZtQ4qFMRe3ltm7yEs56FvmPf4dDqTo0rC4dou9Cp5YLfPvQj8UJdvoEL2RNQXkJra82PYB/?imgmax=800) hoặc hoặc ![clip_image022[1] clip_image022[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhH9o5OPUKKskeFbJrqi9yrdqLNR-iI7wXuz1lugVRqcdqkTmmrcX1DQwu8thyzI5M_rssx_Xd_fqVY9wvMb5XnfrKAkiemQeqqCzTU-6pePltav-V2Qe7qlaF0LkhXR1qIc6Vmc-IqnHlj/?imgmax=800)
| Ví dụ 2 : Giải hệ phương trình sau : 
Đặt S = x + y P = xy Đưa hệ (II) về hệ ![clip_image014[1] clip_image014[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjpe5VmbuwUYEH3UAz38Vcl2ZWLdthV6GeIyRQo4hzolcEGcdWJnh1xv-hiMsegNu0-AquVzB_VQvsutDuAN-imzWcnwxSW1mFB5wUlH9M3qlkaXWCdRI6fD_HvGBemHEscP4tik-1R5-jI/?imgmax=800)
Giải hệ này ta được : ![clip_image016[1] clip_image016[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhaODT6U9nTv2Yz89_R5KIdZP-Y8S5A8mxGwyw4YD8rLzDkDbtcATTH_wqiSHVUjAngFePOeZd9se0jezDHwgkAegUmo4axuGuS4TdHRXbgAheGanZYCdwHnVSmUV_zQXumnKB4sEwO-G6h/?imgmax=800) hoặc hoặc ![clip_image018[1] clip_image018[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgRD3UZFkplREp-uyhxfNoL8rE9PPYQgc8QLKgv_wgEncqDv9X2jAwa2qUWTy-PKMJsOd9_Zw3bzItTvXTiyIg945U4P92aiU_WD5633vUiOBRq7Ju-z2JCn-C4l255pR5ax7EY-_wuo3KW/?imgmax=800)
+Với S = 3 , P = 2 thì được ![clip_image020[2] clip_image020[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgJwVaNyZjtktt88k5M2LpjYljpDf9ed7aX5ywzCZN-ByrbBzRTyCE1I_RGogknw4nN8_0TmAnTmtzXGeUzxjFFDIa4AQ5GrWujFdwHomU70I3VMSfrSnju7wTrXIpYh7xI3CTpoMFcGXE5/?imgmax=800) ; ; ![clip_image022[2] clip_image022[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj9PEJ8RvcKRoqBzOQPRa2Z6mE_PK7JHNaFCpSukYvdOkQ86qNl3DJPb6KxcUQPi9z7TvSCVE3xPBp9V3P67Ryh7-IdKcwPQE5wbJfFvnnPYXCSZpxi_OEiDVKP43fnv_Rex5QSCcL2zFw7/?imgmax=800)
+Với S = -6 , P = 11 thì không có x , y. Kết luận : Nghiệm của hệ (II) là : ![clip_image020[3] clip_image020[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgvVIWayyrgawV1jBOz7xmPi3S4fWIhUKOK_2rviQN1mY_jX4_3qSfzNkvQh7b3hwgB2Hfwi6kX4dbZstmm6NdLQKsmCShXd1wu7TwQ3IeWZjoQtcKf_GOlZojs4GmwhY5nlo8c5pjZ1-3z/?imgmax=800) hoặc hoặc ![clip_image022[3] clip_image022[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjjP8uAGpUriHZPwKBDSHaZFmxC4dr0L7vRDZVSWYBJ2R2G2zE7HuV21VDDWOE57i22leLADKOYnDyAwuc2ejYzoUNPKU2AoyyFZIfbe2Y1Fz08EgZbbFiz2B1wOPFVRtQ4YoBYVP5CZi7M/?imgmax=800)
|
| H3 Tìm quan hệ giữa S , P để hệ phương trình sau có nghiệm : 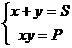
(S , P là hai số cho trước ) | Do ![clip_image026[1] clip_image026[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEguwjUSnORbEWKJNAf-xBierqEGKcHNZuQVlmmPjcQevuFnGnjRzgt6-ieOnlYT7RhCs6bX6pavFv5hn-n0hX4pQufbXD-3vtNzZaeq5qRlpz8naCwJZcflMC8_1jCOVB8HULInExlI2eUX/?imgmax=800) nên x , y là nghiệm của phương trình X2 – SX +P = 0 (1) , hệ nên x , y là nghiệm của phương trình X2 – SX +P = 0 (1) , hệ ![clip_image026[2] clip_image026[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgP_N8JwbisriAwVWKlYluF4z-YoBzntWF8iWCPJRPoevYFcKt1AI7TneSj_B3ZCqkJ-GtKw9LT2JVZ10S31oWYilIBst3svfLs3efk2Yp7sOiyIkAjvjj7GOauztdGh3BQzcCbJjtm51U2/?imgmax=800) có nghiệm khi và chỉ khi (1) có nghiệm , tức là : có nghiệm khi và chỉ khi (1) có nghiệm , tức là : 
| |
| H4: Gọi HS nhóm 3 trình bày hoạt động của nhóm - Em hãy thay x bởi y và thay y bởi x . Hãy cho biết nhận xét của mình ? -Hệ (III) được gọi là hệ phương trình đối xứng . -Nếu (x0,y0) là nghiệm của hệ thì (y0,x0) cũng là nghiệm hệ. -Gợi ý cách giải : lấy phương trình (1) trừ phương trình (2) vế theo vế . 
| -Khi thay x bởi y và thay y bởi x thì phương trình thứ nhất trở thành phương trình thứ hai và ngược lại , phương trình thứ hai trở thành phương trình thứ nhất . -Thực hiện (1) – (2) ta được phương trình : 
Do đó :  hoặc hoặc 
Giải hệ IIIa : 
Giải hệ IIIb : 
Kết luận : nghiệm của hệ là (0,0) (5,5) (-1,2) (2,-1) | Ví dụ 3 : Giải hệ phương trình : 
Lấy (1) –(2) ta được phương trình : (x-y)(x+y-1)=0 
Do đó ![clip_image034[1] clip_image034[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgXiEDGcvmvQ1cT_fpLCkUW58lGJXevbtl-A7Hk46Tpx1_Ehoqdg0Pq2YnvmUTW9qW_CVkslBgCCAz297YSaMXvun28TGM_oKWSYu55loeTMyVKNCnPEaNEbfqDuo9nF_c_zi2LqGBE06j3/?imgmax=800)
hoặc  Giải hệ IIIa ta được nghiệm :  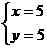 Giải hệ IIIb ta được nghiệm :  
Kết luận : nghiệm của hệ là (0,0) (5,5) (-1,2) (2,-1) |
| H5 Cho hệ phương trình  Biết rằng hệ có 4 nghiệm và 2 trong 4 nghiệm đó là (2,2) và  Tìm các nghiệm còn lại mà không cần biến đổi hệ phương trình . Tìm các nghiệm còn lại mà không cần biến đổi hệ phương trình . | -Dễ thấy hệ phương trình có thêm một nghiệm là (0;0). -Do hệ đối xứng nên hệ có thêm một nghiệm nữa là 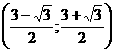 | |
VI/ Củng cố :
Nếu (x0 ; y0 ) là nghiệm của hệ phương trình đối xứng thì (y0 ;x0) cũng là nghiệm của hệ







![clip_image002[1] clip_image002[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjWmZ32af29UAyMAmiLLXL1wxq9f9wdWQyK6uSXh-RLAbklHe3KK7SLLy_WY7kg_MgjHIpcOzb8tGCLXE06oz0ibjGyj-tAJsUG2I3MirIsL6I3oZLw_RFOgawQCmO1q3ZRE3G77eOJ4yAo/?imgmax=800)



![clip_image014[1] clip_image014[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjpe5VmbuwUYEH3UAz38Vcl2ZWLdthV6GeIyRQo4hzolcEGcdWJnh1xv-hiMsegNu0-AquVzB_VQvsutDuAN-imzWcnwxSW1mFB5wUlH9M3qlkaXWCdRI6fD_HvGBemHEscP4tik-1R5-jI/?imgmax=800)






Post a Comment
Bạn có ý kiến thắc mắc hay bình luận gì về bài viết này vui lòng để lại lời nhắn.Cám ơn bạn đã ghé thăm !